Actividad 7 ¡Que divertido trazar diagonales!

Actividad: ¡Que divertido trazar diagonales!

Objetivos: Determinar área del triángulo a partir del rectángulo.

Recursos: El geoplano y ligas de colores.

Desarrollo:

Construye cada rectángulo en el geoplano

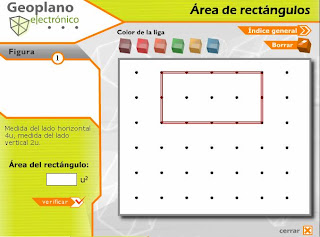
1-      Un rectángulo de cinco unidades de medida de largo por dos unidades de ancho.

2-      Un rectángulo de cuatro unidades de medida de largo por tres unidades de medida de ancho.

¿Cuántas unidades cuadradas tienen cada rectángulo?

Halla el área de cada rectángulo.

Trazar una diagonal dentro de cada rectángulo.

¿En cuántos triángulos se dividieron los rectángulos?

Compara el largo y el ancho de cada rectángulo ¿cómo son?

¿Cómo es el área del triángulo comparada con la del rectángulo?

¿Cuál es área del triángulo ¿explica el proceso aplicado para hallar el área de un triángulo.

 

Actividad 6: Jugando con el tangram construyo el concepto de área

Objetivo: Construir el concepto de área.
Material: El tangram Chino.

Desarrollo

Al pueblo de los malhumorados ha llegado el circo, el alcalde entusiasmado, ha ofrecido dos terrenos, con el fin de que el payaso escoja uno para instalar el circo, el payaso a cambio a ofrecido llenar el corazón de los habitantes de alegría; uno de los terrenos tiene forma triángular y el otro tiene forma cuadrada, payasito no sabe cual escoger, desa el más grande para que los animales estén cómodos.

El alcalde le explica a payasito que el área de los dos terrenos es la misma lo que varía es la forma del terreno, payasito quedó más confundido, no sabe lo que es el área.

Ayuda a payasito:

Toma los dos triángulos pequeños y forma un cuadrado y dibujalo.

Recubre el cuadrado con los dos triágulos pequeños; observa cuántas veces el triángulo pequeño en el cuadrado.

Al recubrir el cuadrado con los triángulos pequeños ¿qué estás haciendo?

¿Qué has medido de la figura?

¿Qué concepto acabas de descubrir con la actividad realizada?

¿Cómo definimos el concepto descubierto?.



Actividad 5: El Rompecabezas Mágico

Objetivo: Describir los esquemas de invarianza y actividad del área mediante el manejo de las piezas del tangram.
Material: Tangram Chino.

Desarrollo: Juan y Ana juegan a armar un rompecabezas que les regalaron, encontraron las piezas sueltas y no saben si están completas. para averiguarlo hay algunas pistas.

Si las piezas están completas deben formar con todas ellas un cuadrado. !Manos a la obra¡

-Diferencia cada ficha con una letra; así:

T = Para triángulos grandes.

M = Para triángulos medianos.

P = Para triángulos pequeños.

C = Para el cuadrado.

R = Para el romboide.

Aplicación

Toma las piezas T une sus lados y forma un cuadrado. Une las piezas restantes y forma un cuadrado.

Explica ¿por qué?

Utilizando el concepto descubierto realiza una actividad parecida a la vivida dentro del aula.

 

Actividad 4 Areas y Perimetros con el Tangram Chino

Objetivos: Calcular áreas y perímetros de figuras sencillas con el Tangram Chino.

Nivel: A partir del tercer ciclo de primaria.

Material: Tangram Chino.

Desarrollo de la actividad

El Tangram es un rompecabezas formado por piezas geométricas: dos triángulos grandes y dos pequeños; un triángulo mediano, uno cuadrado y un paralelo grama.

Con las piezas del Tangram podemos formar muchas figuras. Por ejemplo, un cuadrado:

1- Utilizando el cuadrado pequeño como una unidad de área, calcula:

a)    El área de cada una de las piezas.

b)    El área del cuadrado formado con todas las piezas del Tangram.

2- Utilizando el lado del cuadrado pequeño como unida de longitud, calcula:

a)    El perímetro de cada pieza.

b)    El perímetro del cuadrado formado con todas las piezas del Tangram.

Actividad N° 3 Perimetro con el Geoplano

Actividad sobre perímetro de figuras geométricas utilizando el geoplano.

Materiales: Geoplano  y gomas de colores.

Objetivo: Valorar la importancia del geoplano en la búsqueda del perímetro de figuras geométricas plana

Desarrollo

Los alumnos forman con ligas en su Geoplano un cuadrado como el siguiente:

Calcular el perímetro del cuadrado considerando como unidad de medida la que se muestra en el modelo. P = 4U + 4U + 4U + 4U = 16U

   

Actividad N° 2: Dentro y fuera.

Actividad: Dentro y fuera.

Material: Geoplano, Gomas elásticas de colores.

Objetivo: Descubrimiento de la permanencia de la forma.

Desarrollo: Construir figuras de la misma forma una dentro de otras todas las que sean posibles, habrá entre ellas una única cuadrícula de diferencia con el fin de trabajar la noción de inclusión.

Se les pide a los niños que hagan un cuadrado lo más grande que les sea posible, una vez hecho, pedirles que hagan otro cuadrado también lo más grande posible y así sucesivamente hasta que no puedan hacer más. Variar el color de las gomas para cada figura.

Una vez realizadas, hacer comentarios verbales acerca de la ejecución por ejemplo: ¿De qué color es el cuadrado más pequeño y el más grande? ¿De qué color es el cuadrado que está dentro del cuadrado rojo? ¿Y los que están fuera?

Los alumnos harán comentarios en voz alta sobre las figuras que han hecho, procederán de la misma manera con otras figuras.

Actividad 1: Modelo con el geoplano

Actividad 1  Modelo con el Geoplano

Actividad 1: Cambiando la unidad.

Objetivo: Valorar la importancia de la Geometria para manejar el mundo espacial.

Formados en grupos de cuatro estudiantes realizaran la siguiente actividad:

Formar con ligas en su geoplano cuadrados como estos.

Calcular el perímetro del cuadrado considerando como unidad de medida la que se muestra en el modelo.

Calcular el área y el perímetro de cada cuadrado:

Por ejemplo; el perímetro del cuadrado azul es: P = 5U + 5U + 5U + 5U = 20U

Es decir 20 unidades.

Para medir el área tomamos una unidad cuadrada.

A = 5U X 5U = 25 U²

Es decir el área del cuadrado azul tiene un área de 25 unidades cuadradas.

Concepto de perímetro y área

http://www.uco.es/~ma1marea/Recursos/Geoplano.swf

http://descartes.cnice.mec.es/descartes2/previas_web/materiales_didacticos/geoplano3/geoplano3.html

http://miayudante.upn.mx/actividades/Cisne.htm

http://www.educacionplastica.net/Tangram3.htm

http://www.conevyt.org.mx/cursos/juegos/geoplano/juego.htm

El perímetro de una figura geométrica es el  contorno de la misma y se calcula adicionando las longitudes de cada uno de sus lados.


El área de una figura geométrica es la medida de  una superficie.